关于快慢指针
怎么证明快慢指针在环中是可以相遇的?
证明这个问题?可能你会说,只要快慢两个指针都进入环中,两者有速度差,快指针就一定能够追上慢指针。可是这儿“追上”有可能是两种情况(注意,这儿讨论的是一般情况,快指针步长k >= 2),一是恰好追上(也就是相遇了),二是追上并超过了慢指针。当然,这两种情况都不妨碍我们判断是否有环存在。下面我们就证明一下无论快指针步长k为多少,快慢指针在环中都能恰好相遇。
证明开始:
方法一:
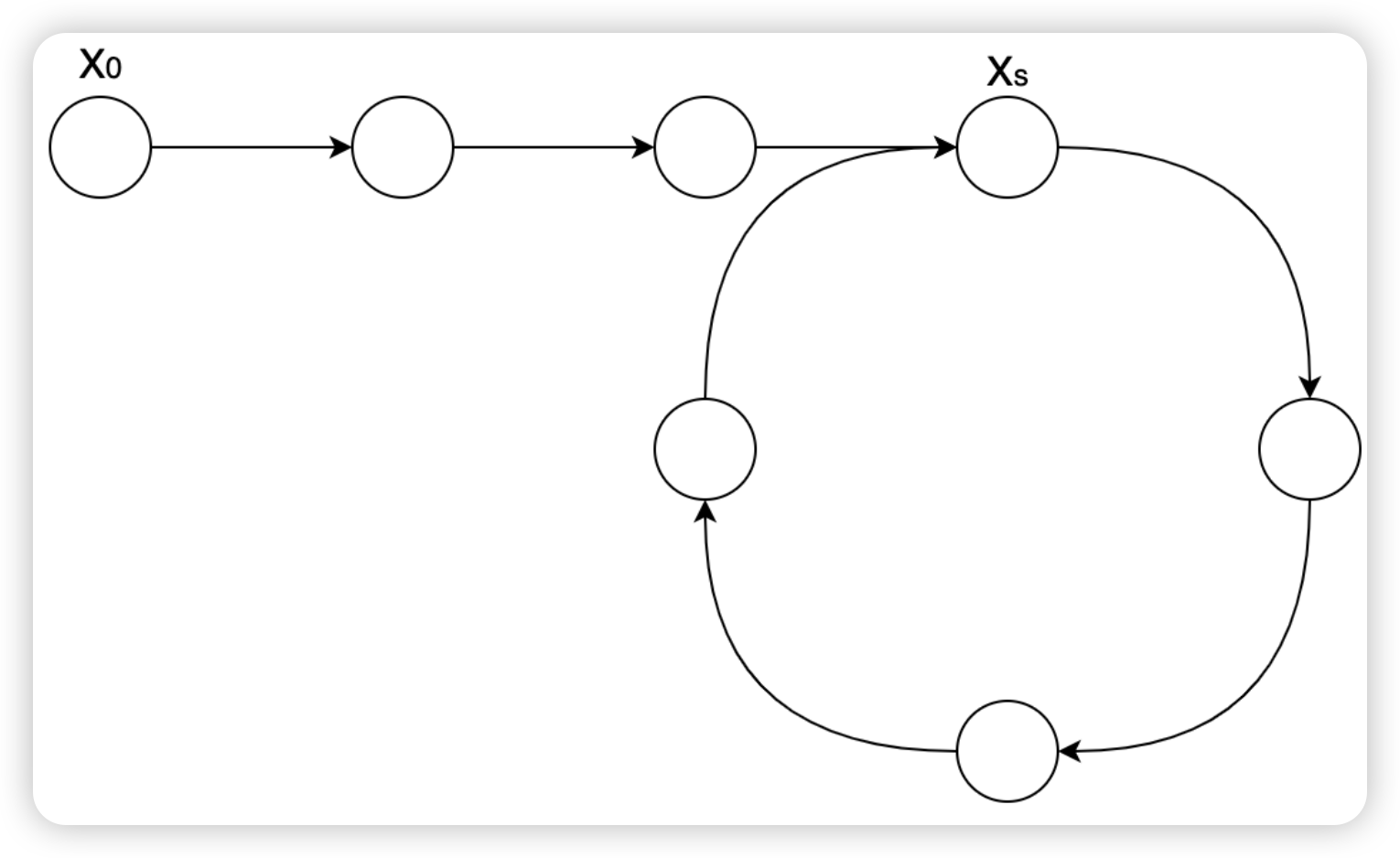
首先,换个角度想问题。用一个步长为1的指针模拟遍历这个单向链表的过程。如上图所示,设单向链表的起始结点为X0(0是下标),环的起始结点为Xs。自然,遍历到最后就是一遍遍的重复这个环。如果,我们把遍历的项都不断记录到一个数组中的话(下标按次序递增),最后就是一定长度的序列串的重复。例如,
X0, X1, … , Xs, Xs+1, …, Xs+cl-1
Xs+cl, Xs+cl+1, …, Xs+2*cl-1
…
cl (circle length)表示环的长度。
假设 j 是 cl 的整数倍,并且是 cl 整数倍中满足 j > s 最小的那个数。对于任意的 k (k >= 2),我们考虑下标分别为 j 和 jk 的两个位置 Xj 和 Xjk。可见,Xj 就是慢指针走了 j 步之后的位置,而 j > s 则保证了此时慢指针已经进入环中。同理,此时的快指针在位置 Xjk,必然也在环中。
因为 j 是 cl 的整数倍,我们可以把 Xjk 看成是一个指针从位置 Xj 开始,走了 (k - 1) 次的 j 步。而每走 j 步,在单向链表的环中,其实又回到了 Xj 位置,因为 j 是 cl 的整数倍。所以我们有,Xj = Xjk 。这样,我们就证明了快慢指针肯定会恰好相遇的问题。
为什么快指针步长要为 2 ?3,4,5可以吗 有了上面证明的基础,就不难发现 k 越小,所需的遍历次数就越少,因为给定一个带环的单向链表,j 的取值是确定的。所以,取 k = 2。当然,除了 1 ,别的其他数都可以。
正规一点儿的分析,如下:
因为 j 是 cl 的整数倍,并且是 cl 整数倍中满足 j > s 最小的那个数。如果 s <= cl,那么 j = cl;如果 s > cl,那么 j < 2*s ,所以 j 的时间复杂度为 O(s + cl)。假设单向链表中结点的个数为 n,因为 s 和 cl 都是小于 n 的,所以 j = O(n) 。这是慢指针的时间复杂度,那么快指针的就是 O(nk) 。所以取 k = 2 ,可以最小化算法的运行时间。
方法二(简单版):
证明能相遇
假定环前节点有 x 个,环上节点有 y 个,快慢指针在环上分别走了 m,n 圈后相遇,
在环上相遇的位置为 z,用 i 表示慢指针在相遇的时候走了多少步。能有如下两表达式:
x + my + z = 2*i + 1
x + ny + z = 1*i
两式相减
(m - n)y = (2-1)i + 1
说明 i+1 的值为环节点长度的倍数,即可相遇
为什么快指针步长要为 2 ?3,4,5可以吗
有了上面证明的基础,就不难发现 k 越小,所需的遍历次数就越少,因为给定一个带环的单向链表,j 的取值是确定的。所以,取 k = 2。当然,除了 1 ,别的其他数都可以。
正规一点儿的分析,如下:
因为 j 是 cl 的整数倍,并且是 cl 整数倍中满足 j > s 最小的那个数。如果 s <= cl,那么 j = cl;如果 s > cl,那么 j < 2*s ,所以 j 的时间复杂度为 O(s + cl)。假设单向链表中结点的个数为 n,因为 s 和 cl 都是小于 n 的,所以 j = O(n) 。这是慢指针的时间复杂度,那么快指针的就是 O(nk) 。所以取 k = 2 ,可以最小化算法的运行时间。
总结:取其他数可以,但每取大一倍数就得多走一圈,所以取2才是最优解。
参考: